Abaqus基于内聚力理论的光圆钢筋与混凝土粘结性能研究及敏感性分析

有限元法和界面元法是研究钢筋–混凝土粘结性能的常用数值模拟方法。建立了锈蚀钢筋混凝土粘结滑移模型并探究二者间的粘结性能。分别利用有厚度内聚力建模方法和无厚度内聚力建模方法探究钢筋–混凝土之间的粘结性能。建立考虑冻融损伤的粘结滑移模型并对RC梁试件的地震破坏过程进行模拟。考虑钢筋混凝土的粘结滑移，研究灌浆套筒连接装配式混凝土梁柱节点在低周反复作用荷载下的抗震性能。建立CFRP加固钢筋混凝土方柱三维细观数值模型，研究了不同工况下钢筋混凝土方柱的抗震性能，提出了CFRP加固混凝土方柱名义抗剪强度尺寸效应理论公式。通过钢筋混凝土构件的爆炸实验得出考虑粘结滑移效应的有限元模型能更好的体现钢筋混凝土构件的宏观力学行为。对轨道板–CA砂浆层间界面本构行为进行研究，揭示层间离缝机理提出了一种改进指数型界面内聚力模型。拓宏亮等(拓宏亮,etal.2021)基于内聚力本构关系,发展了复合材料静力和高周疲劳分层本构模型。针对钢筋混凝土梁裂纹扩展问题,介绍了一种内聚力模型的方法来模拟钢筋混凝土梁在静态条件下的断裂行为。利用内聚力开裂模型模拟 CFRP 界面层的剥离过程。通过上述近期文献调研可以发现，目前对内聚力模型的研究大多以二维模型为主，很少有人研究三维有限元模型中网格尺寸和内聚力参数对钢筋–混凝土粘结滑移行为的影响。

 

本文以钢筋–混凝土粘结滑移模型为研究对象，采用内聚力理论，以粘结段长度为分析对象

建立钢筋–混凝土粘结滑移有限元模型，并试验曲线进行对比分析，发现曲线拟合效果较好。在此基础上，以不同直径的钢筋作为分析对象，探究不同钢筋直径下的钢筋与混凝土之间的粘结性能。通过数值模拟的方法，将钢筋的位移量和位移时间作为输入层，将钢筋的荷载作为输出层，建立预测钢筋混凝土粘结–滑移行为的机器学习模型，以期为数值研究钢筋混凝土粘结滑移行为提供一个可靠且快速的分析手段。

 

2. 内聚力模型

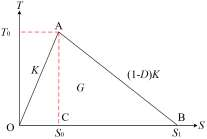
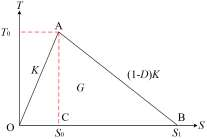
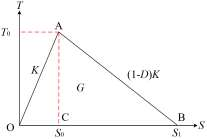
内聚力的发展主要分为三个阶段，分别为弹性变形的牵引-分离阶段、损伤起始阶段和损伤演化阶段。六面体内聚力单元如图 1 所示，双线型内聚力本构模型的损伤演化响应图如图 2 所示。图 2 中，横坐标 S 为损伤位移，纵坐标 T 为损伤强度。其中，T0 为损伤起始强度，对应 A点；S0、S1 分别为损伤起始点和损伤失效点所对应的位移，分别对应 C 点和 B 点；K 为弹性阶段的刚度，对应线段 OA 的斜率；G 为整个损伤阶段产生的能量，对应三角形 OAB 的面积；D 为损伤变量，(1-D) K 代表内聚力单元刚度的折减，对应线段 AB 的斜率。由图 1—2 可以看出，当内聚力单元中应力满足损伤起始准则时，相邻的两个单元之间开始开裂并进入损伤演化阶段。随着两个单元的位移逐渐增加，内聚力单元应力逐渐降低，当达到一定位移时，单元间的内聚力彻底消失，裂纹的扩展也随之终止。

 

 

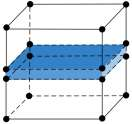
图 1. 六面体内聚力单元

 

 

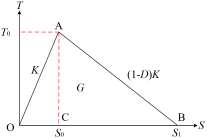
图 2. 双线型内聚力本构模型

 

 

1. 牵引–分离定律

牵引–分离定律 (Tension–separation law) 用于描述

 

 

 

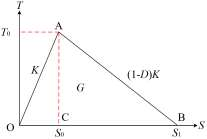
图中 OA 段的内聚力单元的弹性变形，其主要目的是建立牵引力与单元分离度之间的内在

联系。当一个内聚力单元分离度达到一个特定材料的损伤起始位移 S0 时，材料之间的粘结力开始减弱。牵引–分离定律的本构关系通常定义为：

 

 

 

式中，t (MPa) 为内聚力单元应力矢量，由法向应力分量 tn (MPa)、第一切向应力 ts (MPa) 和第二切向应力 tt (MPa)组成；K(TN•m-3)为内聚力单元弹性刚度，由法向刚度 Knn (TN•m-3)、第一切向刚度 Kss (TN•m-3) 和第二切向刚度 Ktt (TN•m-3) 组成；δ (‰) 为内聚力单元应变矢量，由法向应变分量 δn (‰)、第一切向应变分量 δs (‰) 和第二切向应变分量 δt (‰) 组成。

 

2. 损伤起始阶段

损 伤 起 始 准 则 是 描 述 材 料 点 开 始 表 现 损 伤 行 为 的 判 定 依 据 ， 即

 

 

 

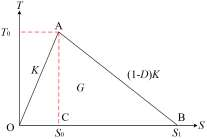
图中的 A 点。为了更好地探究内聚力单元的应力关系，采用二次名义应力准则 (Quadratic

nominal stress criterion) 作为损伤起始的判断依据：

 

 

 

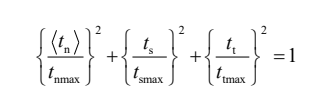
式中，tnmax、tsmax 和 ttmax 分别为纯法向、第一剪切方向和第二剪切方向内聚力单元所能承受的最大应力 (MPa)。

 

3. 损伤演化阶段

损 伤 演 化 规 律 用 于 描 述 损 伤 起 始 后 内 聚 力 单 元 刚 度 退 化 的 规律 ， 即 对 应 于

 

 

 

图中的 A 点。为了更好地探究内聚力单元的应力关系，采用二次名义应力准则 (Quadratic

nominal stress criterion) 作为损伤起始的判断依据：

 

 

 

式中，tnmax、tsmax 和 ttmax 分别为纯法向、第一剪切方向和第二剪切方向内聚力单元所能承受的最大应力 (MPa)。

 

3. 损伤演化阶段

损 伤 演 化 规 律 用 于 描 述 损 伤 起 始 后 内 聚 力 单 元 刚 度 退 化 的 规 律 ， 即 对 应 于

 

 

 

图中 AB 段的斜率。该阶段通过引入损伤变量 D，描述内聚力单元刚度的退化过程。为了完整描述损伤演化阶段，在损伤起始并逐渐积累的过程中，损伤变量 D 的取值从 0 单调地演化增加到 1，从而判定材料的完全失效。为了更加合理地描述损伤演化过程，采用基于能量的损伤演化 (Energy-based damage evolution) 模型，其表达式为：

 

 

 

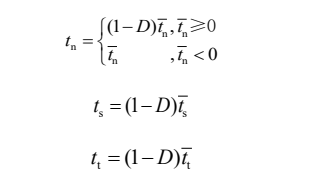
式中，`tn、`ts 和`tt 分别为不考虑损伤情况下由牵引-分离定律本构关系计算得到的法向应力分量(MPa)、第一切向应力分量 (MPa) 和第二切向应力分量 (MPa)。

 

3. 钢筋–混凝土粘结滑移行为的有限元模型

本文主要采用牟晓光 (牟晓光 2006) 的钢筋混凝土局部粘结–滑移试验数据，对基于ABAQUS的钢筋混凝土粘结–滑移有限元模型进行内聚力参数标定。为了避免动态响应的影响，数值仿真采用准静态加载方法。钢筋混凝土粘结–滑移模型如图 3 所示。其中，混凝土块的尺寸为 150 mm×150 mm×150 mm，钢筋的长度和直径分别为 200 mm 和 9 mm。

 

为了监测钢筋相对混凝土的相对滑动值，在钢筋加载端设置力面耦合点 RP–1，详见图 3 (a)。因此可将 RP–1 作为滑移监测点，通过有限元计算得到该点的位移和反力值，获得钢筋混凝土粘结–滑移行为的荷载–位移响应曲线。加载端以位移方式进行加载，加载位移为 3 mm，分析步稳定时间为 1×10–10 s。为保证数值模拟结果的准确性，分别在加载端和自由端加入了 PVC 套筒，钢筋两端的非粘结段套在 PVC 套筒中，从而防止在拉拔过程中加载端应力过大，避免混凝土发生局部破坏而导致预测结果不准确。此外，钢筋中间的粘结段长度为 45 mm，粘结段在中间应力分布更均匀。混凝土块四周节点设置固定约束，为避免模型表面约束点处翘曲变形过大导致网格划分不准确，将混凝土几何模型划分为八等份，然后进行相应的网格离散。其中，混凝土的网格尺寸为 6 mm，钢筋的网格尺寸为 5 mm，网格类型均为六面体。

 

 

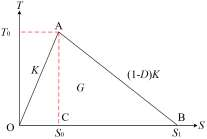
图 3. 钢筋混凝土粘结–滑移模型

 

考虑实际工程中钢筋混凝土之间没有厚度，故选用无厚度内聚力建模方法(surface–based

cohesive behavior)，旨在钢筋与混凝土之间赋予内聚力行为，从而当钢筋和混凝土发生相对滑动时，进而在界面处产生粘结力，即钢筋表面的剪应力。

 

表 1. 有限元模型材料参数

 

 

表 2. 内聚力参数

 

 

其中，内聚力参数中损伤起始强度 T 和能量 G 根据 Yuan (Yuan 2004) 和吴业飞 (吴业飞2010) 给定的解析公式和参数范围进行取值，其中能量 G 的取值范围为 0.5 N/mm–1 N/mm，当G 在给定的拟合参数范围内，T 为较大值可以准确地得到其它试件的极限荷载，解析公式详见式1、2 和 3。刚度 K 依据宋启根 (宋启根 1981) 的混凝土界面层刚度约为混凝土弹性模量的 75%的结论进行取值。

 

 

 

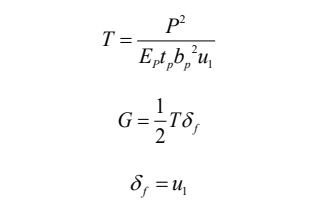
式 1 中，T 为损伤起始强度 (MPa)、P 为钢筋的极限拉拔荷载 (kN)、Ep 为钢筋的弹性模量 (×104 MPa)、tp 为混凝土块的厚度 (mm)、bp 为钢筋直径 (mm)、u1 为钢筋加载端极限滑移量 (mm)。

 

式2中，G 为钢筋与混凝土界面产生的最大断裂能 (N‧m–1)、d f为钢筋加载端极限滑移量 (mm)。

 

对本文建立的有限元仿真模型的预测结果与牟晓光 (牟晓光 2006) 的试验结果进行了对比，并绘制了钢筋混凝土粘结-滑移行为的荷载-位移响应曲线，结果如图所示。由图 4 可以看出，有限元模型预测得到的光圆钢筋荷载–位移曲线预试验结果的吻合效果较好，荷载增加和峰值点过后的下降趋势基本相同。值得注意的是，有限元模型预测峰值点后曲线下降幅度略高于试验，这是由本文采用了形式更为简单且参数更少的双线型内聚力本构模型。如果未来研究中需要更多地关注峰值点后下降段部分，可以通过采用指数型内聚力本构模型，描述钢筋混凝土粘结–滑移行为的损伤演化规律。虽然内聚力双线型、指数型和梯形本构分别对应着不同的损伤演化阶段，但这三种本构模型得到的曲线发展趋势基本相同 (Cornec 2003)。

 

 

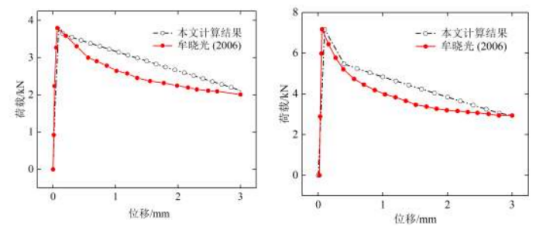
(a) 粘结段为 5 倍直径的对比图 (b) 粘结段为 10 倍直径的对比图

图 4. 有限元模型与试验结果的钢筋混凝土粘结–滑移行为的荷载–位移响应对比图

 

4. 不同钢筋直径对混凝土粘结性能的影响

为了更好的探究钢筋与混凝土之间的粘结性能，特选取钢筋的荷载–位移曲线作为判断钢筋与混凝土之间粘结性能的标准，本节主要选取粘结长度为 5 倍直径，探究不同直径的钢筋的荷载–位移曲线的发展趋势。其中，混凝土的模型尺寸为 150 mm×150 mm×150 mm，钢筋的直径分别为 6 mm，7 mm，8 mm 和 12 mm，长度为 200 mm。模型的加载条件和约束条件详见图 3。四种不同直径的钢筋混凝土粘结滑移模型网格划分图和应力云图如图 5，6 所示。

 

 

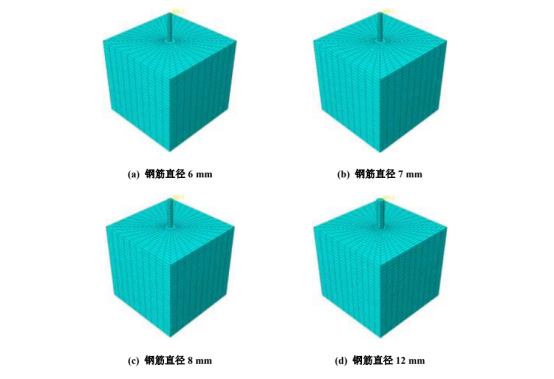
图 5. 不同钢筋直径的钢筋–混凝土粘结滑移模型网格划分图

 

 

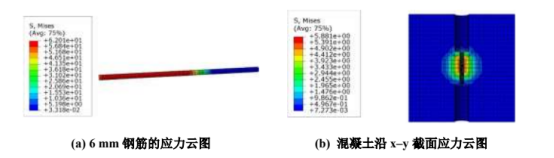
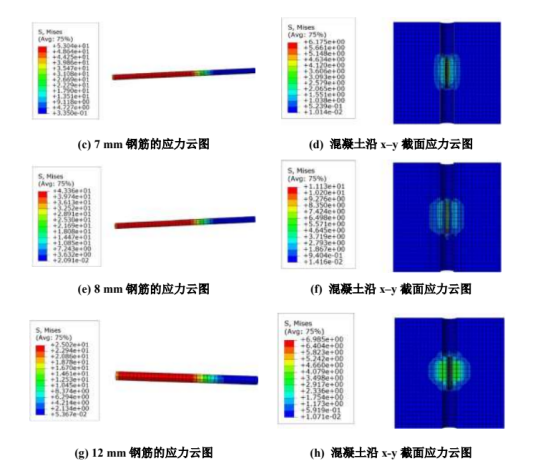
图 6. 不同直径的钢筋混凝土粘结滑移模型的应力云图

 

四种不同直径的钢筋所得到的荷载–位移曲线如图 7 所示。通过荷载–位移曲线形式可以看出，随着钢筋直径的增加，钢筋的极限拔出荷载逐渐增加。这是由于钢筋直径的增大，导致钢筋与混凝土发生粘结滑移的接触面积增加，使得其粘结强度降低，钢筋的极限拔出荷载值增大。同时，通过荷载–位移曲线可以明显看出曲线的发展趋势相同，符合典型的荷载–位移曲线的发展趋势，更加有力地说明了有限元模拟结果的可行性。

 

 

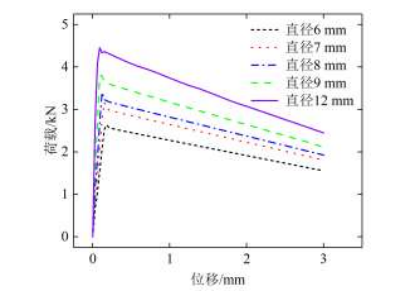
图 7. 不同直径的钢筋的荷载–位移曲线

 

5. 内聚力参数敏感性分析

针对钢筋混凝土粘结–滑移模型，以钢筋直径为 9 mm 的模型、粘结长度为 5 倍直径的工况为例，从曲线的力学形态角度，探究有限元模型的内聚力参数敏感性，三种内聚力参数在不同数值下所对应的荷载–位移曲线关系如图 8 所示。

 

 

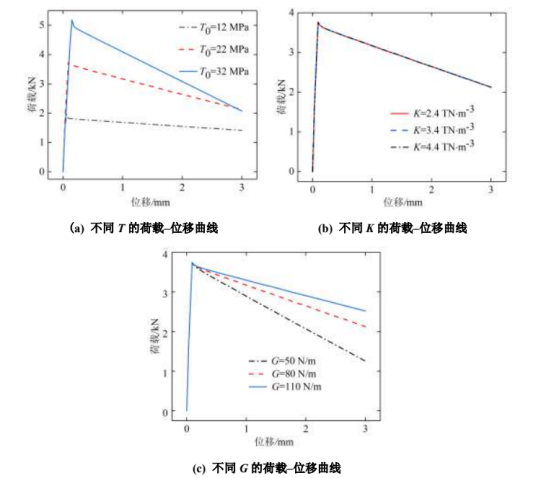
图 8. 内聚力参数对荷载–位移曲线的影响

 

从图 8 (a)可以明显看出，在刚度 K 和断裂能 G 相同的情况下，荷载峰值点随着损伤起始强度 T0 的增加而增加。造成这种现象的原因是：相同的外部荷载给予模型相同的能量，T0 过大使荷载峰值点提高，该能量不能维持峰值点后的斜率下降速度正常。当 T0 过小时，引起荷载峰值点下降，这是由于内聚力单元承载的能量过大，进而引起下降段的曲线斜率大于正常的下降段曲线斜率。

 

由图 8 (b)可以看出，刚度对曲线的整体趋势几乎没有影响，K 的大小仅仅对曲线峰值点有非常小的影响；峰值点随着 K 的增加而略微提高，但其影响基本可以忽略不计。这是因为：T0 影响材料刚度 K，当能量 G 不变时，在荷载–位移曲线的弹性阶段，随着 T0 值的增大 K 值呈线性增大的趋势 (吴业飞等 2010)。因此，当 T0 和 G 保持不变时，K 值的变化对荷载–位移曲线的弹性阶段几乎没有影响。在拉拔过程中，钢筋混凝土粘结部分由于粘结力的作用使混凝土逐渐产生微裂纹。因此，混凝土界面层刚度比混凝土的弹性模量要低一些，其值约为混凝土弹性模量的75%，符合文献 (宋启根 1981) 对刚度 K 取值定义。类似地，由图 8 (c)可以看出，G 对峰值点前的斜率和曲线峰值点几乎没有影响，G 值的增大引起峰值点后下降段斜率的减小。

 

6. 结论

本文采用内聚力理论建立不同直径的钢筋混凝土粘结–滑移模型，从细观角度探究二者间的粘结性能。通过引入无厚度内聚力建模方法进行三维模型的建立，利用空间轴对称模型模拟钢筋与混凝土之间的粘结滑移，通过将数值模拟与物理试验测出绘制的荷载–位移曲线进行耦合对比，发现该方法的仿真度较高，与实际出入不大，并且还能够进一步测算出试验无法直接观测的数据。

 

对光圆钢筋进行不同直径的模拟，钢筋直径分别取 6 mm、7 mm、8 mm、9 mm 和 12mm，随着钢筋直径的增加，其极限拔出荷载值越大。从粘结–滑移响应曲线的力学形态研究发现，有限元预测模型对内聚力主要参数的敏感程度从大到小的顺序依次为 T0、G 和 K。其中，T0 影响曲线的峰值点以及峰值点后下降段斜率，G 对峰值点后下降段斜率影响较大，K 对曲线力学形态的影响几乎可以忽略不计。

 

资料来源：达索官方