基于 Abaqus 子程序的颗粒材料成型过程仿真

简介

颗粒材料成型是指在特定的压力、温度等工艺条件下，将金属、合金或非金属的颗粒状材料，加工成某种特定形态的过程。常用的颗粒材料包括：金属、合金材料，如铁基、镍基、钛合金、钴铬合金、铝合金材料，药物粉末，陶瓷粉末等。

 

颗粒材料的成型工艺主要有注射成型和压缩成型。注射成型即将粒状喂料加热至一定高的温度使之具有流动性，然后将其注入模腔中冷却下来，得到所需形状的、具有一定刚性的坯体，然后将其从模具中取出，得到成型坯体的过程。压缩成型又分为模压成型和等静压成型，模压成型过程是将干粉状坯料在固定形状的模具中，压制成致密坯体的一种成型方法；等静压成型是在一定温度与压力条件下，粉料的各个方向同时均匀受压受热的成型工艺 。

 

颗粒材料的成型包含以下三个过程：

（1）粒子重排靠近机制：颗粒之间排列松散，存在许多孔隙，颗粒间大多呈点状接触，压力作用下，一些颗粒被压入附近空隙，变形的阻力较低；

（2）塑性变形阶段：颗粒之间排列松散，存在许多孔隙，颗粒间大多呈点状接触，压力作用下，一些颗粒被压入附近空隙，变形的阻力较低；

（3）扩散蠕变阶段：残余气孔弥散分布在基体中，致密化机制变为单个原子或空穴的扩散蠕变。

 

基于以上成型机理，颗粒材料成型仿真是极为复杂的非线性过程。零件变形通常约有30%或以上，具有大位移和大应变的几何非线性特征；需考虑弹性、塑性变形，以及高温作用下的蠕变机制，需要材料具有复杂的非线性特性；颗粒材料和模具之间的接触位置和接触状态不断的发生着改变，属于边界非线性。

 

因此，进行颗粒材料成型过程仿真，需要选择合适的本构模型来描述颗粒材料的变形机理，并要求求解器具有准确、高效的非线性计算能力。

 

颗粒材料本构模型

本文假设颗粒材料为带有相对密度这一变量的连续体，采用宏观模型来近似描述颗粒材料在成型过程中的特性。

 

非线性弹性模型

假设颗粒材料的弹性过程为分段的各向同性弹性材料，每段均满足胡克定律，图 1 为颗粒材料单轴压缩过程的应力-应变曲线，从曲线可以看出，加载、卸载阶段，均存在弹性变形，且随着轴向压力与密度的变化，材料的弹性参数也随之变化。因此，本文将材料弹性阶段的参数设为随密度、轴向应力变化的函数。

 

 

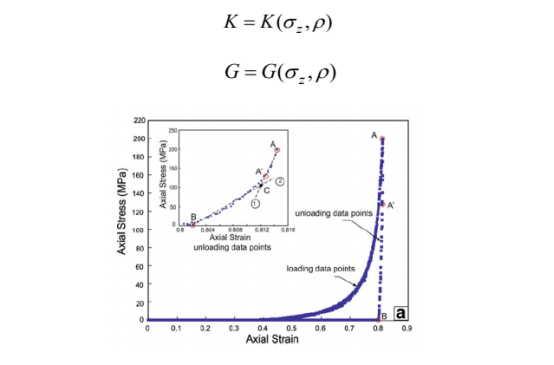
图 1. 颗粒材料单轴压缩过程加载卸载曲线，图片来源于文献(L.H.Han,2008)

 

Modified Drucker-Prager Cap (MDPC)模型

Drucker-Prager/Cap 模型演变自 Mohr-Coulomb 屈服准则，自 20 世纪 50 年代以来不断被修正。本文采用 Modified Drucker-Prager/Cap（MDPC）模型，如图 2 所示，该模型分为剪切破坏面（Fs）、盖帽面（Fc）和过渡面（Ft）。剪切破坏面可控制材料在剪切作用下的屈服行为，盖帽面可以控制材料在压缩作用下的屈服，同时还可控制材料的无限剪胀，过渡面光滑地连接剪切破坏面和盖帽面，便于进行数值计算。目前该模型广泛应用于各种粉末材料的压缩模拟。

 

剪切破坏面的表达式如公式（3）所示，其中 d 为内聚力，β 为摩擦角，p 为静水压力，q 为 Mises 等效应力。

 

 

 

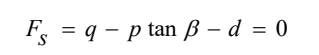
盖帽面的表达式如公式（4）所示，参数 R 控制帽盖面的几何形状，一般取值在0.0001~1000 之间，参数 α 控制过渡面的形状，一般取值在 0.01~0.05 之间，其数值由用户指定。pa为盖帽面和过渡面交点所对应的 p 值。

 

 

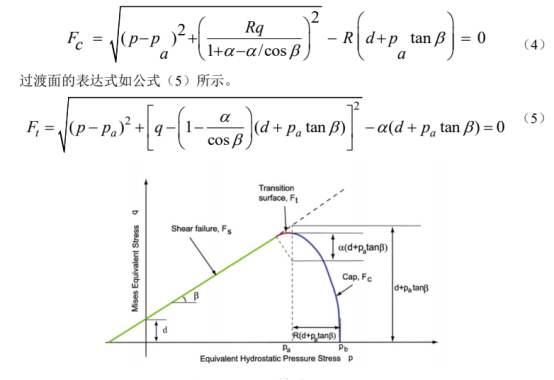
图 2. MDPC 模型屈服面

 

此外，由于颗粒材料在成型过程中，相对密度发生了很大变化，且材料的屈服条件、硬化规律等都与相对密度有关，因此仿真分析时应考虑相对密度的影响情况，本文将MDPC 模型的各参数均定义为密度相关的函数。图 3 显示了密度对 MDPC 模型屈服面的影响情况。

 

 

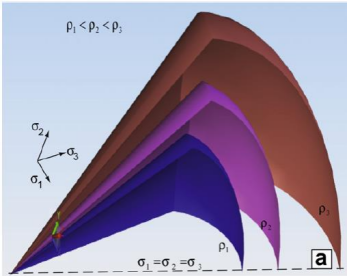
图 3. 不同密度下 MDPC 模型的屈服面

 

Abaqus(V)USDFLD 子程序

使用 Abaqus 软件中自带的 Elastic 模型和 Cap Plasticity 模型，可以实现上述弹性阶段和塑性阶段 Modified Drucker-Prager/Cap（MDPC）模型参数的定义，通过 Cap Hardening命令，还可以定义颗粒材料的硬化规律，即屈服应力随非弹性体积应变的变化规律。但由于采用软件默认方式，Elastic 模型和 Cap Plasticity 模型中各参数均为固定值，无法模拟材料参数的密度、应力相关性，因此，需要使用(V)USDFLD 子程序接口，定义材料参数随密度和应力的变化规律。

 

(V)USDFLD 子程序简介

(V)USDFLD 子程序介绍如下：

l(V)USDFLD 子程序通常用于需要建立复杂材料模型，而用户又不希望开发 UMAT

或 VUMAT 子程序的的情况；

l该子程序将材料性质定义为场变量的函数；

l允许用户在单元的每个积分点定义场变量值；

l子程序可以访问求解的结果数据，即材料属性可以是结果数据的函数。

 

(V)USDFLD 子程序的应用

分别将颗粒材料的相对密度和轴向应力定义为(V)USDFLD 子程序中的场变量 field(1)和 field(2)，各材料参数为场变量的函数，并通过表格的形式在 Edit Material 界面进行定义，计算过程中，子程序的调用顺序如图 4 所示。

 

 

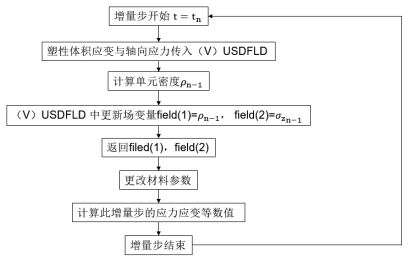
图 4. (V)USDFLD 子程序调用过程

 

应用案例

案例 1——MCC Avicel PH101 药物粉末压缩成型

有限元模型

· 参考文献(L.H.Han,2008)中的计算模型，使用圆柱形模具进行压制，模具半径为4mm，如图 5 所示；

· 粉末材料使用轴对称单元，模具采用解析刚体进行建模；

· 模拟过程包括压制和脱模：压缩速度为 0.1mm/s，粉末材料高度由 6mm 压缩至2mm，随后移走 upper punch，lower punch 向上将压制好的药片推出模具；

· 材料参数的数值，参考文献(L.H.Han,2008)中的实验数据进行拟合（因只有图片可参考，因此数据存在误差）；

· 粉末与壁面的摩擦系数取 0.2；

· 分别计算不同初始密度下，分析粉末材料在成型过程中密度、应力等数值的变化情况；

· 分别采用了 Abaqus/Standard 和 Abaqus/Explicit 求解器进行计算

 

 

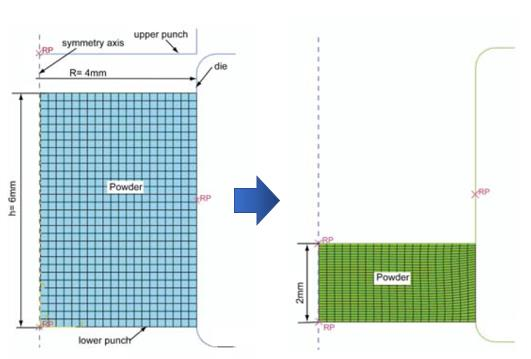
图 5. 案例 1 有限元模型

 

仿真方法可信性验证

图 6 为成型过程的密度-压力曲线，通过隐式分析结果与文献(L.H.Han,2008)提供的密度载荷曲线对比可知，本文的仿真结果与文献(L.H.Han,2008)结果吻合良好。此外，密度云图显式，受壁面与粉末材料的摩擦力影响，靠近壁面的位置会出现密度不均匀现象，这种现象与文献(L.H.Han,2008)中的密度云图一致；应力云图显式，在脱模阶段，由于位于模具外部片剂的径向回弹，靠近模具边缘的粉体会出现高应力区域。

 

密度和应力的不均匀现象，会导致三种典型缺陷：剥落、脱顶和分层（如图 9 所示），这与实际情况相符。但因无法获取准确的材料参数，因此密度、应力的结果数值会有所偏差。

 

 

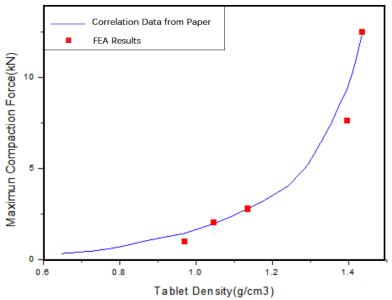
图 6. 密度压力曲线（隐式分析）

 

 

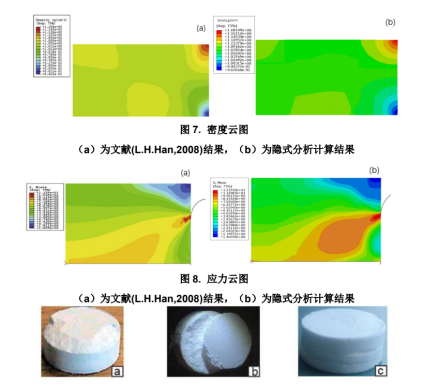
图 9. 片剂的典型缺陷（a）剥落（b）脱顶（c）分层

 

隐式分析与显式分析结果对比

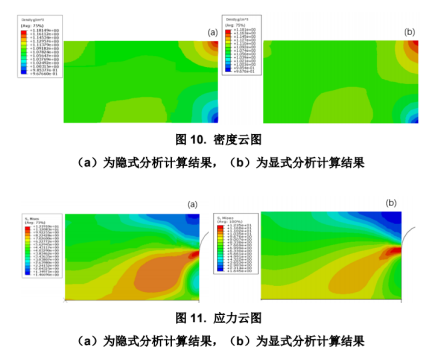
图 10 与图 11 为隐式分析与显式分析结果的对比，由结果可知，初始密度和材料参数相同时，两种分析方法得到的密度、应力分布形式基本一致。最大密度误差为 0.003%，最大应力误差为 1.3%。

 

因此，该材料模型具有可信性，且隐式分析与显式分析方法均可使用。

 

 

 

案例 2——高温合金粉末热等静压分析

有限元模型

为了进一步拓展此仿真方法的使用范围，案例 2 分别采用了 2D 模型与 3D 模型进行计

算，模型说明如下：

l2D 模型：

根据模型的对称性，采用 2D 轴对称单元进行建模；

约束模具对称轴位置，在模具外表面按时间顺序同时施加温度和压力载荷；

l3D 模型：

根据模型的对称性，截取模型的四分之一进行建模；

约束模具对称轴位置，在截面位置施加对称约束；

l粉末材料使用文献(胡建召,2017 )中 W_Cu20 合金材料参数，材料参数具有温度、密度的相关性；

l在模具外表面按时间顺序同时施加温度和压力载荷，工艺过程曲线如图 13 所示，其中各时间节点的意义为：a 第一次加温加压结束，b 第一次保温结束，c 第二次保温结束，d 冷却至室温；

l粉末与模具间摩擦系数设为 0.05；

l采用 Explicit 分析方法；

l分析类型为热力耦合分析。

 

 

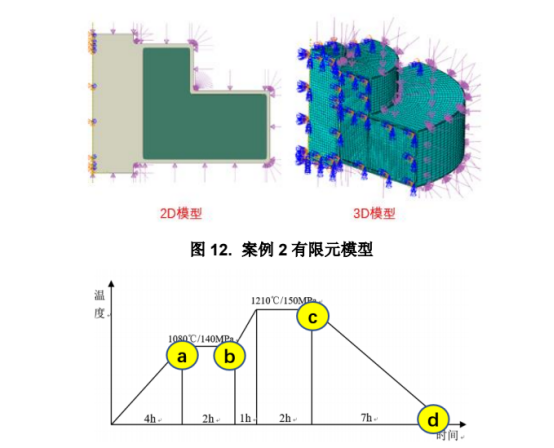
图 13. 工艺过程曲线

 

结果说明

图 13 中工艺过程曲线中各时间节点对应的密度结果如图 14 和图 15 所示，由结果可知，第一次保温结束时，粉体的相对密度基本已达到 0.9 以上，在第二次保温结束时，粉体相对密度基本达到 0.95~0.999，仅在凸角处由于边角效应，相对密度低于 0.9，这与实际情况相符。

 

对比 2D 模型和 3D 模型的密度结果，可以看出，3D 模型上半部分相对密度值略低于2D 模型的结果，两种模型相对密度随时间的变化趋势基本相同。

 

此外，冷却至室温时，3D 模型中粉末材料的截面尺寸与 2D 模型基本相同。粉末材料的主体区域应力分布均匀，且应力值较小，3D 模型与 2D 模型的应力结果较为一致，仅在局部应力集中位置，最大应力误差为 6.4%。

 

因此，可以将上述颗粒材料的建模方法应用在 3D 模型上，这为复杂零部件的仿真设计提供了参考。

 

 

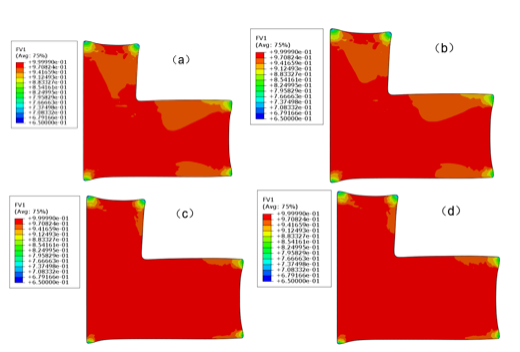
图 14. 2D 模型密度云图

 

 

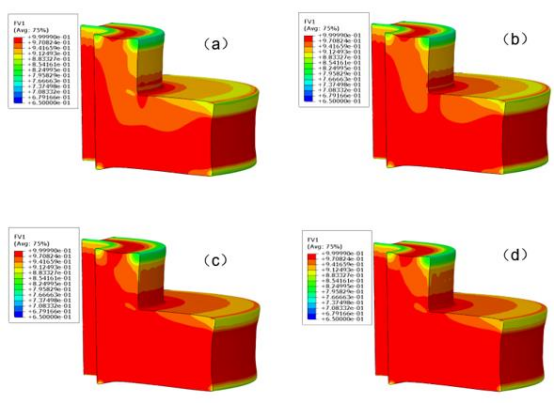
图 15. 3D 模型密度云图

 

 

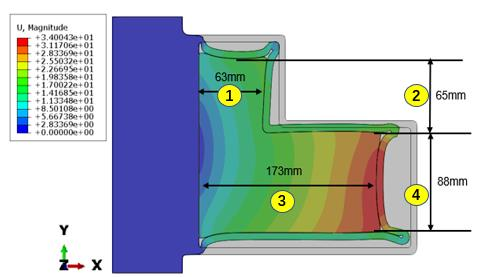
图 16. 2D 模型最终尺寸

 

 

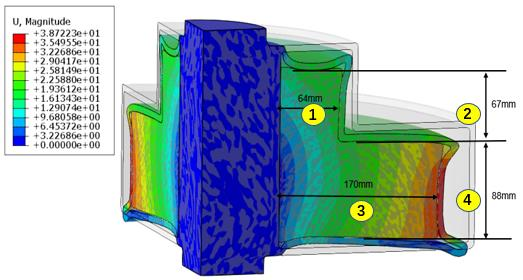
图 17. 3D 模型最终尺寸

 

 

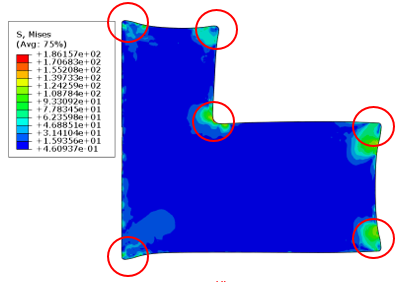
图 18. 2D 模型应力云图

 

 

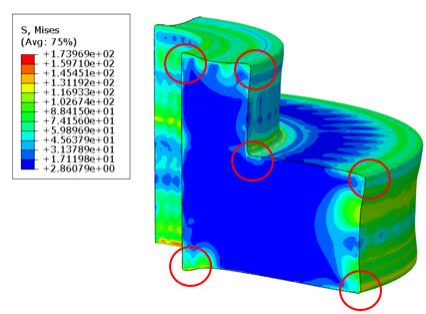
图 19. 3D 模型应力云图

 

结论

本文基于生产实际需求，结合文献，进行了颗粒材料成型仿真分析研究，利用 Abaqus软件的子程序功能，建立了与密度、应力相关的 Modified Drucker-Prager/Cap 本构模型，来模拟颗粒材料。

 

通过案例 1，可知该材料模型与文献结果吻合良好，验证了此仿真方法的可信性（包括隐式分析与显式分析），通过案例 2，将该方法推广到了 3D 模型，可以更好的满足实际零件的设计需求。

 

资料来源：达索系统