直接循环分析
产品：Abaqus/Standard Abaqus/CAE
概述
直接循环分析：
l 是一种准静态分析；
l 使用傅里叶级数和非线性材料行为的时间积分相结合，迭代获得结构的稳定循环响应
l 避免了与瞬态分析相关的大量数值费用；
l 非常适合非常大的问题，其中许多负载循环必须应用到获得稳定的响应，如果进行瞬态分析；
l 可采用线性或非线性材料进行局部塑性变形；
l 可用于预测塑性棘轮行为的可能性；
l 假定几何线性行为和固定接触条件；
l 使用弹性刚度，因此方程组只反演一次；
l 也可用于预测延性散装材料的渐进损伤和失效，和/或预测低周疲劳分析中层合复合材料界面的分层/脱粘增K
参考资料：
l 定义分析
l *直接循环
l 时间点
l 控制
l 配置一个直接循环过程
介绍
众所周知，在多次重复加载循环后，弹塑性结构的响应，如承受较大温度波动和夹紧载荷的汽车排气歧管，可能会导致稳定状态，在每个连续循环中的应力一应变关系与前一个相同。获得这种结构的响应的经典方法是重复施加周期性负载的结构，直到获得稳定状态。这种方法可能是相当昂贵的，因为它可能需要许多加载周期的应用之前，得到稳定的响应。为了避免与瞬态分析相关联的相当大的数值开销，可以使用直接循环分析来计算循环结构的直接响应。该方法的基础是构造一个位移函数u(t)来描述结在一个周期为T的荷载循环中所有时刻t的响应，如图1所示。
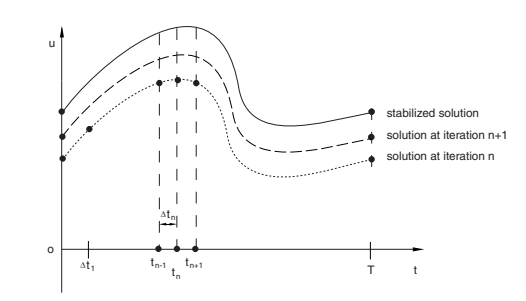
图一：在周期为T的荷载循环中，在不同的迭代中，r时刻的位移函数。
为此目的使用截断傅立叶级数
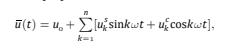
其中n为傅里叶级数中的项数W=2/是a ngular频率，把你，微克，a和Uf是与问题中的每个自由度相关的未知位移系数。Abaqus/Standard通过使用修改后的牛顿法求解未知的位移系数，在分析步骤开始时的弹性刚度矩阵作为方案中的雅可比矩阵。我们用与位移解形式相同的傅立叶级数展开修正牛顿法中的剩余向量
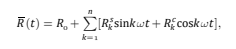
其中傅立叶级数中的每个剩余矢量系数R、R和R分别对应于位移系数u、u和uf。剩余系数通过跟踪整个负载周期而获得。Abaqus/Standard在循环中的每一个瞬间通过使用标准元素逐元素计算获得剩余向量R (t)，当在整个循环中积分时，提供傅立叶系数。
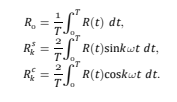
位移解是通过求解对应于缓存剩余系数的位移Fourier系数的修正来获得的。在下一次迭代中使用更新后的位移解，得到timc中各时刻的位移。重复这个过程，直到获得收敛。在整个负载循环过程中自动传递因此，可以被认为是非线性问题解的一次迭代。通过确保剩余系数的所有条目都很小来衡量收敛性在直接循环算法中详细描述了获得稳定循环的算法。
温馨提示：
此文档为达索官方英文文档翻译，尽管我们已经尽力确保准确性，但在翻译过程中可能会有一些错误或细微差别。如果想要了解官方原版，可联系客服进行索取。
