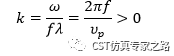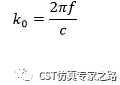18620856065
广州思茂信息科技有限公司
索 取 报 价
资   讯   中   心​
 

CST软件如何获得色散图 Dispersion Diagram --- 区分波数k与相位常数beta

来源: | 作者:thinks | 发布时间: 2023-10-01 | 3176 次浏览 | 分享到:

相信接触过Dispersion Diagram色散图的朋友一开始都会有同样的疑问，色散横坐标到底是什么？

 

上网一搜Dispersion Diagram，能见到wave number, wave vector, propagation constant, phase constant, phase, phase advance, phase shift per cell, β, β(rad/m), β*d, βp, βL/2π,  k，kz，还有-π~π，0-180-180-0, 0-π-sqr(2)π-0, Γ-X-M-Γ,  Γ-K-M-Γ  等等等等，或者CST本征模求解器的结果：0-1-2-3或frequency。

 

你就说头大不?

 

其实要搞清楚这些表达式的区别很容易，在我看来，他们。。。都一样。

 

首先分清楚两个量，波数k和相位常数beta，直接上我的总结：

 

字母

β                                  

k

名称

相位常数

Phase Constant

波数

Wave Number

等效名称

（条件）

传播常数（无损）

Propagatoin Constant

波矢（加方向）

Wave Vector

单位

rad/m

rad/m

定义式

（右手材料，向前传播）

 

 

定义式变式

 

（右手材料，向前传播）

 

 

 

 ω角频率单位rad/s,

 相速度单位 m/s。

 

 

 

ω角频率单位rad/s,

  相速度单位 m/s。

特殊值

 

（可叫Light line或Air line ）

 

 

c: 光速

 

 

c: 光速

周期结构的单元长度

d （也可以叫p，L, a等等）

 

d（也可以叫p，L, a 等等）

 

周期结构

单向传输

双向平面

CST 求解器

+ unit cell边界参数扫描

+  unit cell边界参数扫描

推荐求解

Mode数量

1

>=2

扫描角范围

单一方向扫相位0-180

 

X和Y两个方向扫相位

（布里渊区）

CST 扫描参数

Phase

PathPara

CST 模板默认扫描范围

5-175, step =10

0.1-2.9, step =0.28

CST 扫描结果

扫描之前运行宏：

“Define Slow Wave userdefined Watch

直接扫描

色散图

        ω vs β 

f vs Γ-X-M-Γ

色散图：色散工程中是指k或beta与频率的曲线；根据表中的变式，这条曲线的系数就是相速度Vp决定，还可以通过曲线的斜率判断群速度Vg，非常方便。

 

所以，色散曲线的横坐标就是k或beta，下面我们研究一下，为什么横坐标会有这么多的表达方法：

 

1.    Beta相位常数

Beta是指单方向传播电磁波，单位距离的角相位，我们更关心以该单元为周期结构时，传播的特性：比如相速度Vp。

 

之前写过两个传输性质的单元结构，传输线单元和行波管单元：

 

仿真实例019：行波管TWT仿真（上）慢波结构的冷设计

仿真实例050：微带传输线 - 本征模 - Beta相位常数，色散图, 相速度, Pierce耦合阻抗

 

比如其中传输线单元原始结果和调整后的结果：


 

 

 

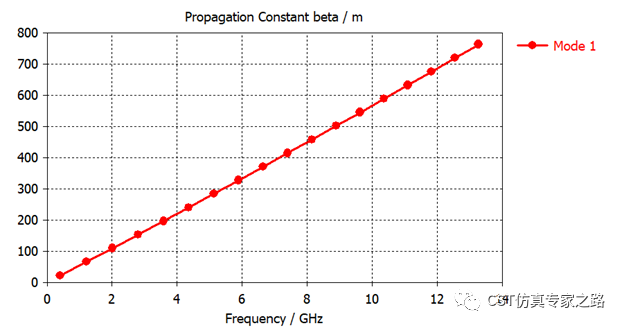
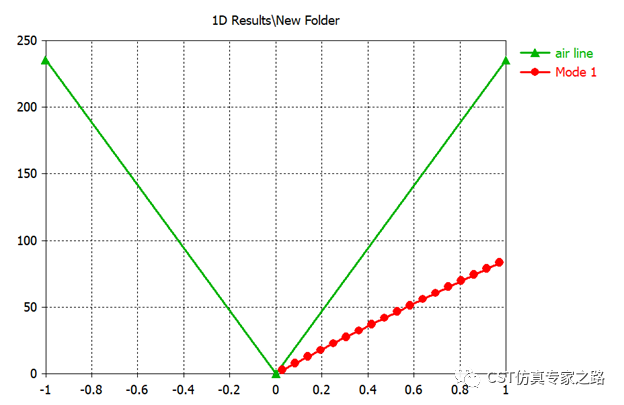
传输线的色散线是直的，斜率为正，所以群速度相速度同方向，为右手材料；若为左手材料，比如之前写的SRR，模式曲线可以向下倾斜（扯远了, 以后再说）。

 

传输线单元和行波管单元两个案例都是只有在传播方向上是周期边界而已，所以扫描角度0-180度，具体如何将CST直接的propagation constant beta/m vs frequency的结果转化成 

ω vs β 的方法也在文章中。

 

beta作为坐标轴的几种表示方式：

 

· 

Beta本身单位是rad/m, 这时横坐标数值不限。

· 

其他表示方式: k, Wavevector (10^4 m^-1)， Wave number(β), Wave number(um), β=2pi/lamda (cm-1) 等等。

 

· 

Beta*d就是一个单元长度下的相位，单位是rad；这时横坐标就可以是负π到π。

· 

· 

其他表示方式: β*d, βd(rad/m),  β*p, βp, β*period (degrees), kL, ka, kd 等等。

 

· 

Beta*d/π 就是一个单元的一个π内的相位数，可以叫归一化的beta，无单位；这时横坐标就可以是-1到1。

· 

· 

其他表示方式:   β(π/d),  phase/π,  k(π/a)， KL/ π等等。

 

2.    k波数

k是指平面360度周期方向，单位距离的角相位，我们更关心以该单元为周期表面时，该表面横向的特性，比如就是模式间的禁带。

 

之前写过两个平面性质的单元结构，光子晶体单元和蘑菇形单元：

 

仿真实例015：超材料光子晶体和禁带分析实例

仿真实例051：超表面---经典蘑菇型结构的AMC特性与EBG特性

 

比如其中蘑菇形单元原始结果和调整后的结果：


 

 

 

 

 

 

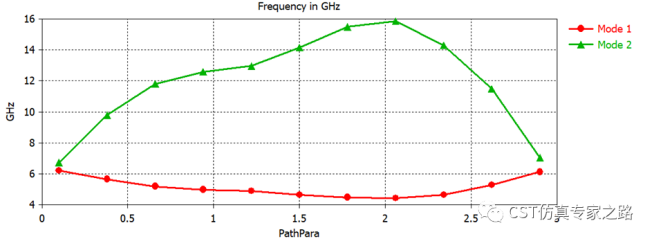
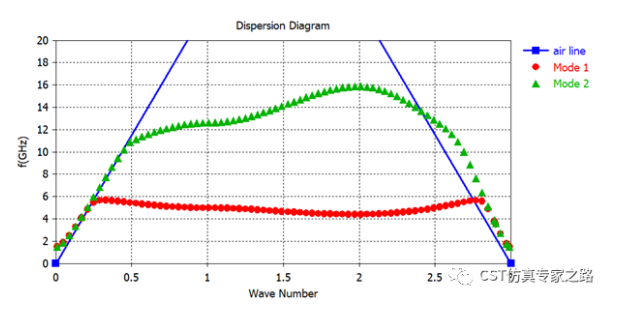
光子晶体单元和蘑菇形单元两个案例都是看两个横向的模式，所以扫描角度要包括XY平面一周，这就是布里渊区的作用，通过扫描

(phaseX= 0~180, phaseY=0)

(phaseX=180, phaseY=0~180)

(phaseX=180~0, phaseY=180~0)

 

三个区间就可以表征360度一圈每个角度。这三个区间等于CST中的0-1-2-3。

 

其实细心的朋友应该能发现，这三个区间的第一个区间，就等于X方向上的beta色散。

 

 

小结：

1.    色散图首先搞清楚是扫描一个方向还是两个方向，是k和beta。

2.    可在CST中手动加空气线（光速线）作为色散图标准尺。

3.    可见很多时候k和beta混着用，所以只要自己知道自己在干什么就可以了。

4.   这里为了简单，本文中用的都是普通的右手材料，左手材料的色散以后有机会再写。懂了色散图，左手材料就很容易学习了。

5.   本文中的布里渊区 Γ-X-M-Γ是假设X和Y方向90度角的周期排列。60度角以后再写。

 

（内容、图片来源：CST仿真专家之路公众号，侵删）

 

版权与免责声明：

凡未注明作者、来源的内容均为转载稿，如出现版权问题，请及时联系我们处理。我们对页面中展示内容的真实性、准确性和合法性均不承担任何法律责任。如内容信息对您产生影响，请及时联系我们修改或删除。

 主 营 产 品
Abaqus
cst
cst
Abaqus
Xflow​
Powerflow
Powerflow
Xflow
CATAIA
simpack​
simpack
CATIA
最 新 内 容
热 门 文 章
知 识 科 普
方 案 解 析
  • 汽车交通
  • 风能电源
  • 船舶机械
  • 生物医疗
  • 土木建筑
  • 新能源
  • 高科技
行业资讯
CST
abaqus