对高速球轴承较突出的热问题进行分析需要知道球在内外圈滑动摩擦规律。经典准静态分析理论基于套圈控制假说，对球轴承中球的滑动分析并不准确。本文用 ABAQUS 对高速混合陶瓷球轴承进行动力学仿真分析，得到球在内外圈滑动规律。
1 介绍
Jones的经典套圈控制假说有争议，且与试验不大符合。相比钢球轴承，高速旋转的陶瓷球的离心力要小40%，使得对于钢球轴承来说的高速（例如 1M DN）工况，对混合陶瓷球轴承来说可能只是中速，套圈控制假说可能并不适用。而且对于中速工况的钢球轴承，套圈控制假说不适用，基于该假说的经典准静态方法也就不适用了。
非线性有限元分析软件 ABAQUS 能方便的仿真包含摩擦和离心作用的高速动力学问题。本文主要目标是用ABAQUS 对高速混合陶瓷球轴承进行动力学仿真，获得接触角、接触载荷、旋滚比、自旋摩擦功率等结果，然后将这些结果与基于套圈控制假说的准静态理论计算的结果（以下简称准静态理论值）对比。
2 有限元模型
使用商业非线性有限元分析软件 ABAQUS 对混合陶瓷角接触球轴承进行显式动力学分析，所用轴承几何尺寸参数和材料参数分别见表 1 和表 2。
表 1 几何尺寸
表 2 材料参数
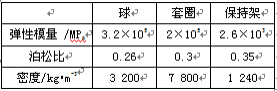
为方便分析而采取的模型简化：
（1）只施加轴向载荷；
（2）陶瓷球的杨氏模量是钢套圈的 1.6 倍，因此将陶瓷球简化为解析刚体，并在球心位置处定义点质量单元，球的质量和转动惯量定义于该点质量单元。该简化使球与套圈的接触应力可能偏大、接触变形可能偏小，但对球与套圈的接触力、接触角以及球的运动影响很小。本文主要是获取接触角、接触载荷以及球运动等参数，接触应力和接触变形完全可以用接触载荷和接触角等参数通过静态分析方法获得精确值；
（3）保持架由于几何形状复杂，不方便定义为解析刚体，本文将之定义为离散刚体以减少计算量；
（4）球与套圈、球与保持架之间的摩擦定义为库仑摩擦，摩擦系数取两个固定值：0.05 和 0.11 以分别仿真两种不同的润滑。
边界条件：外圈底平面固定，内圈和保持架只保留轴向转动与轴向移动两个自由度。接触：定义球与内外圈、球与保持架的接触，接触属性里的库伦摩擦系数分别定义为 0.05 和 0.11。网格和单元：由于球与套圈接触区域狭长，需要对内外圈进行局部网格细化，所选单元为增强沙漏控制、二次精度的 8 节点三维实体减缩积分单元（C3D8R），划分了网格的模型见图 1，内外圈的单元数共为 430 000。分析步：为考虑离心效果，选取显示动态分析步，第一步加载轴向载荷，第二步用角加速度的方式加载内圈转速至规定值，第三步匀速转动。
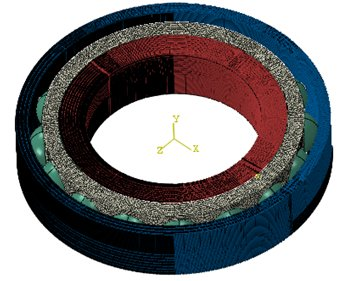
图 1 角接触球轴承 FEM
3 结果与分析
取轴向载荷为 16 和 24kN、内圈转速为 10、16、20、25k rpm、摩擦系数为 0.05 和 0.11 进行分析，稳定运转阶段的球轴承球与内外圈的接触载荷、球角速度等参数是平稳波动的，分别取平均值，并做相应处理，所得结果如图 2 至图 8。
图 2 示出球与内外圈接触载荷的 FEA 值和准静态理论值吻合。滑动摩擦系数对球与内外圈接触载荷的 FEA值影响不大。
图 3 示出球与内圈接触角的 FEA 结果与 Harris 准静态理论结果接近，球与外圈接触角的 FEA 结果小于 Harris准静态理论结果。滑动摩擦系数对内外圈接触角的 FEA 值影响不大。
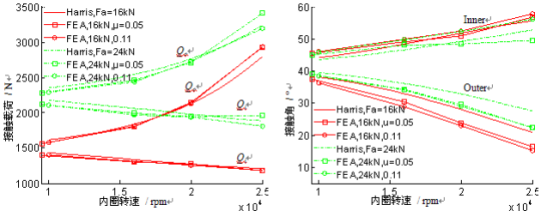
图 2 接触载荷随内圈转速变化 图 3 接触角随内圈转速变化
图 4 示出球公转角速度 mn （即保持架转速）的 FEA 值与 Harris 准静态理论值吻合较好。滑动摩擦系数 m 对球公转角速度的 FEA 值影响不大。
图 5 示出球自转角速度 nb 的 FEA 值小于 Harris 准静态理论值， nb 的 FEA 值与 Harris 准静态理论值随内圈转速和轴向载荷的变化趋势一致。滑动摩擦系数u对球公转角速度的 FEA 值影响不大。
图 6 示出随着转速的增加，Pitch angle 的仿真值趋近于 Harris 准静态理论值。滑动摩擦系数u对Pitch angle的FEA值影响不大。
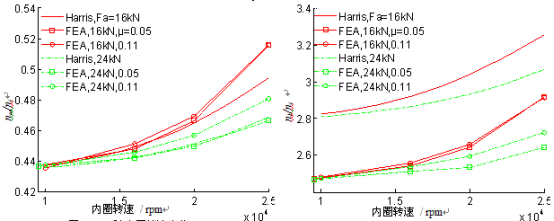
图 4 nm/ni 随内圈转速变化 图 5 nb/ni 随内圈转速变化
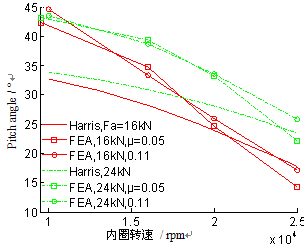
图 6 Pitch angle 随内圈转速变化
图 7、8 示出球与外圈滚道接触处的旋滚比并不为零（理论认为是零）。当轴向载荷为 16kN 且内圈转速小于12k rpm 时，球与内圈滚道接触处的旋滚比小于球与外圈滚道接触处的旋滚比，套圈控制假说并不适用于这些工况。摩擦系数对球与内外圈旋滚比的 FEA 值影响不大。
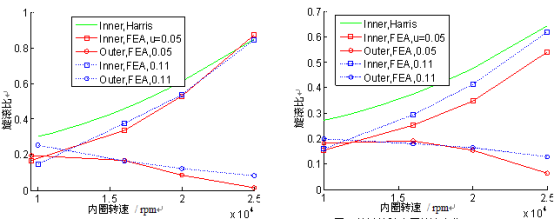
图 7 旋滚比随内圈转速变化, Fa=16kN 图 8 旋滚比随内圈转速变化, Fa=24k
4 结论
本文提出的运用有限元法对高速混合陶瓷角接触球轴承进行显式动力学仿真是成功和有效的。球与内外圈接触载荷、接触角、球公转角速度、Pitch angle 的仿真值与 Harris 准静态理论值吻合。仿真和 Harris 准静态理论计算的球自转角速度、球与内圈旋滚比随内圈转速和轴向载荷的变化规律一致。轴向载荷从 16kN 到 24kN、内圈转速从 10krpm 到 25krpm，球与外圈接触处旋滚比不为零且不容忽视，球在外圈自旋摩擦功率虽小于球在内圈自旋摩擦功率但也不容忽视。Harris 准静态理论对整个轴承的自旋摩擦功率的估计值偏低。
摩擦系数对接触角、接触载荷、球公转和自转角速度、Pitch angle、内外圈旋滚比的 FEA 值影响不大。
资料来源：达索官方
