粘胶的动态力学性能对终端产品可靠性的影响越来越重要。基于 Abaqus 的超弹性加粘弹性的本构模型定义了光学胶的动态力学参数，利用 Abaqus/显式分析进行了静态压缩和落球试验的仿真分析，并对仿真分析结果和实际试验结果进行了对比验证。结果表明，在准静态到高应变率的范围内，采用超弹性加粘弹性的本构可以准确地描述光学胶的动态力学行为。
随着消费电子产品的功能集成化、复杂化的过程中，大量的结构连接通过粘胶粘接来实现。在当前最热的移动终端市场，智能手机、平板电脑等结构中均出现了大量的粘胶，粘胶材料的动态力学行为对结构可靠性的影响也越来越大。因此在结构仿真中，对粘胶材料动态力学行为定义的准确性对结构仿真结果的影响变得越来越重要。
常见的粘胶为高分子材料，一方面高分子材料均具有非线性的弹性行为和大变形特性—超弹性特性[1]；另一方面，高分子材料的力学行为均表现出显著的时间相关性—即率相关性[2]。高分子材料力学行为的复杂性，导致当前还不存在一个物理意义明确，同时既可以描述高分子材料超弹性又可以准确描述率相关性的本构模型。当前对高分子材料超弹性的描述应用比较广泛的是建立在唯象理论基础上的应变能密度函数模型[3]。而对材料力学行为的率相关性定义的方法通常有两种：（i）以不同应变率下的材料变形行为为基础，通过对不同应变率的力学行为进行插值而获得材料的率相关特性[4]；（ii）以特定与时间无关
力学行为基础—基准，通过引入与时间相关的函数方法对基准力学行为进行与时间相关的缩放，从而实现材料力学行为的率相关性描述[5]。本文选择了一种常见的光学胶为研究对象，基于 Abaqus 的超弹性和粘弹性材料模型定义了光学胶的动态力学性能，通过静态压缩和动态落球测试的仿真与试验对比，对基于 Abaqus 超弹性和粘弹性理论模型对光学胶动态力学行为定义的有效性和准确性进行了探讨和分析。
1 试验方法
1.1 静态压缩试验参数
测试设备：岛津 AG-50kNX 万能试验机，压缩速度为 0.1mm/min，样品尺寸：10×10×1mm 1.2 动态落球测试参数动态落球测试在自制的落球测试系统完成，如图 1 所示。
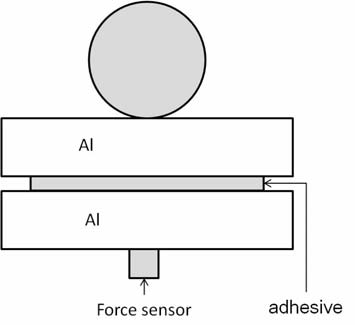
图 1 动态落球测试系统示意图
落球测试系统为三明治结构，光学胶由上下两个垫块夹持，落球在对上垫块施加一个冲击载荷，光学胶作为载体，在下垫块处产生一个冲击力，在下垫块处通过力传感器采集该动态冲击力信号。落球高度不同，则施加在光学胶上冲击压缩速度不同，从而在光学胶上产生不同冲击压缩速率作用，从而实现光学胶的不同应变率下的变形工况。本研究中具体动态落球测试参数见表 1。
表 1 动态落球测试参数
2 仿真建模
2.1 材料模型
本文中选用的材料模型为 Abaqus 提供的超弹性(hyperelastic)和粘弹性(Viscoelastic)理论模型。超弹性参数描述了材料在静态变形过程中的非线性弹性行为；而粘弹性参数的引入，在此起到一个随应变率缩放的效应，从而实现材料力学性能与时间相关的率相关性。
Abaqus 中对超弹性材料模型的定义存在多种应变能函数形式[6]：Mooney-Rivlin，Odgen，多项式等。本文选则的模型为 Marlow 模型，直接采用测试数据定义即可。本文中光学胶超弹性的定义由单轴静态压缩数据进行定义。Abaqus 对率相关性定义的粘弹性材料模型是通过松弛函数—Prony 级数[6,7]来定义：
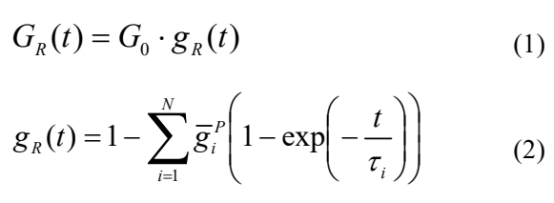
式中：G0—分别为瞬态剪切模量；
GR(t)——t 时刻的剪切模量；
τi —松弛时间；
gi—松弛系数；
上式中 τi，gi 被称为 Prony 系数。
在 Abaqus 中对时域粘弹性材料模型的定义有四种方法：动态频率谱参数法、应力松弛测试参数法、蠕变测试参数法和 Prony 系数法。本研究中对光学胶粘弹性参数通过动态频率谱参数来定义。
2.2 仿真模型
本研究中静态压缩和动态落球仿真均采用Abaqus/Explicit 分析。由于光学胶的大变形特性，选择的单元类型为 C3D8R，加沙漏控制。
3 结果与讨论
3.1 静态压缩仿真与试验
采用 Abaqus/Explicit 分析进行了光学胶静态压缩仿真，计算时间为 20ms。考虑到准静态分析的目的，在压缩仿真时，不考虑材料力学性能率相关特性，因此材料卡片的定义不包括粘弹性(率相关性)定义部分。图 2 为静态压缩仿真与试验的对比结果。从图中可以看出，仿真结果与试验结果几乎完全重合，表明超弹性模型对该光学胶非线性力学行为的定义和描述非常准确。
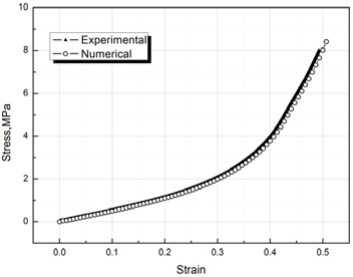
图 2 静态压缩仿真与试验结果对比
4.2 动态落球仿真与试验对比
为了验证光学胶动态力学行为定义的准确性，本文采用自制的动态落球系统进行了实际测试和仿真对比验证。通过调整落球高度，实现光学胶在不同应变率下的冲击压缩工况。图 3 为不同高度落球试验与仿真结果的对比。从图中可以看出，随着跌落高度的增加，落球系统的接触反力峰值增加，同时冲击振动的周期减小。通过仿真与试验结果的对比可以发现，在应力波的周期、峰值两方面仿真和实验结果均吻合较好。同时存在三个方面的小差异：
一、在落球高度比较低时（5mm，10mm），在起始阶段仿真和实验的冲击波重合性很高，而在 15mm 和 20mm 落球时，冲击波起始阶段存在一定差异；
二、峰值存在差异，仿真结果均大于实验结果；
三、应力波的下降阶段均存在偏差。对于第一个差异点，这可能与仿真接触定义有关，上垫块和光学胶的刚度差异较大，而本研究中采用了简单的通用接触，并没有对其接触刚度约束进行详细的定义，接触阻尼等也没有考虑，因此在仿真结果中，冲击振动起始阶段存在一些微小偏差。对于第二个差异点，而对于仿真与实验结果峰值的差异，在整个落球试验仿真系统中，除粘胶引入粘弹性特性以外，落球系统其他组成部分的材料阻尼、结构阻尼等没有被考虑，因此导致了仿真结果比实验结果在峰值上存在一点差异。差异点三，应力波下降阶段在落球试验的过程中反映的是光学胶压缩中的回弹阶段，这个结果表明当前光学胶参数定义中其加载阶段比较准确，但是其卸载行为还存在一定的偏差。这个问题主要是由于光学胶的非线性力学行为的复杂性引起的，在高分子材料的加载和卸载过程中，由于 Mullins 效应[6]的存在，其加载路径和卸载路径并不重合。在 Abaqus 中关于高分子材料Mullins 效应的定义提供了理论模型，但是由于其无法与率相关性(粘弹性)同时使用，在本研究中没有引入。
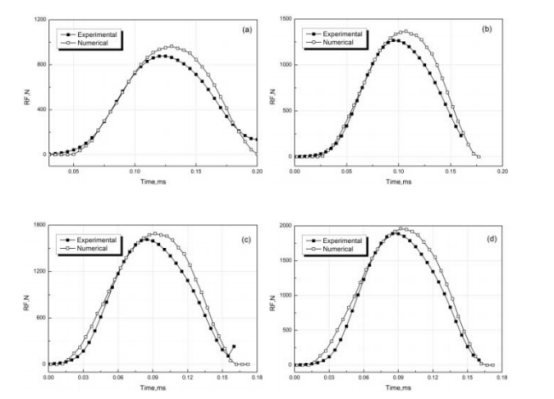
图 3 不同高度落球试验与仿真结果对比
(a)5mm;(b)10mm;(c)15mm;(d)20mm
在前面仿真与试验对比的基础上，图 4 给出了在准静态压缩和动态落球时光学胶压缩变形的应变率分析结果。在静态压缩过程中，光学胶压缩变形的应变率为 0.00167s-1；动态落球仿真分析中，随着落球高度增加，光学胶的最大冲击应变率增加，落球高度为 5mm 时，光学胶的最大压缩应变率为 18/s；跌落高度为 20mm 时，光学胶的压缩应变率最大值接近 50/s，光学胶变形的应变率在 10~50s-1 量级，此结果表明本落球系统有效的实现了光学胶在高应变率下变形。结合两者的应变率分析和仿真与试验对比分析，在准静态到高应变率变形的范围内，基于 abaqus 超弹性和粘弹性定义的光学胶力学参数有效的且准确地描述了光学胶的动态力学行为，试验与仿真结果均吻合较好，充分说明基于 Abaqus 的超弹性加粘弹性模型的本构定义，可以准确地描述光学胶的动态力学行为—非线性和率相关性。
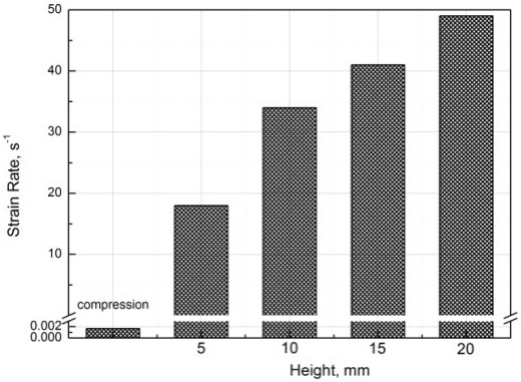
图 4 不同工况下光学胶变形应变率对比
资料来源：达索官方
